(This is the part 3 of discussion of realSEUDO).
When the activation profiles are generated, there are different ways to scale them that basically depend on how do we normalize the reference images of the cells.
For example, apparently one traditional way is to normalize them is to make the sum of all the pixel values to be equal 1. A consequence of this is that the larger cells have more bleak reference
images, and so their found coefficients for least-squared-error fit to match the same absolute brightnesss in the frame will be higher, since the formula is basically (coefficient = frame_brightness / reference_image_brightness).
The SEUDO (noise suppression) algorithm does a different normalization: it considers the cell image as a multi-dimensional vector (with each pixel being a dimension) and normalizes it to the euclidean length (i.e. norm2) of 1. This way all the cell images and all the gaussian kernels (that get normalized in the same way) have the same euclidean length and duke it out being equal in this parameter. But it still means that the larger cells will have more bleak images with the same consequences, although less so than in the first kind of normalization.
The differing coefficients mean that the activation profiles of different cells are not really comparable, they will be scaled all differently. It also means that as the cell images are being learned and change frame-to-frame, the coefficients they produce in the recognition part will differ wildly. RealSEUDO solves the last problem by generating the update coefficients for the previous frames as the learning happens. Fortunately, the updates are easy: since the reference images are scaled by a multiplier, they recognition results can be easily adjusted by changing this multiplier (which for them is actually a divisor, since the relation is reciprocal).
But I think that in general the property of
comparability between different cells and between different recordings
is very important, and nobody seems to pay much attention to it. From the mathematical standpoint it's "we can always normalize to the mean and variance". But that normalization works only if we have seen all the cells reach the same maximal absolute brightness. If some cell never reached more than half that, the normalization will make it twice brighter than it was. But if in some session it never reaches more than half brightness and in another session it lights all the way up, its profiles not only won't be comparable to the other cells but even to the same cell in another session. That's why I think that we should look for some absolutes.
The differing coefficients also create a different way of inequality in recognition: the larger cells with higher coefficients get an advantage in LASSO and experience a weaker push towards 0, and the gaussian kernels, being usually smaller than even the small cells, get a stronger push towards 0. Which might be good or not. I haven't experimented with this, so I don't know which way is better in reality, but it definitely looks like something worth experimenting with.
To make the profiles comparable, I think the right way is to put them into the range between 0 and 1, at least more-or-less. The easy way to look at it is that we take the range of pixel brightness and remap it to [0, 1], then we take the brightest activation of a cell and rescale its brightness so that the brightest saturated pixels also become 1. Then the maximal coefficient also becomes 1. There are a couple of problems left though.
First, it might affect LASSO, and a different scaling might work better for LASSO. This is easy to solve: since the coefficient changes reciprocally to the scaling of the reference image in normalization, LASSO can be run with one kind of normalization and then a single multiplication operation can convert it to another kind.
Second, there is the problem of noise, at both the low and high ends. At the low end the black isn't black, it's a kind of frothing gray with some level of background lighting. At the high end there are very bright pixels that go above the normal brightness. At the low end realSEUDO makes an assumption that the cell activations aren't very dense, and so the median pixel brightness in the image represents the close-to-average average background lighting, and then the difference between that and the 10-percentile brightness represents the level of background noise (although these levels may need to be adjusted if the assumptions are incorrect, and there is also an adjustment for unevenness of background lighting). So we take this difference and go up by that much from the median to cut the noise off, and that becomes our 0 level. At the high end it collects the brightest levels of every pixel that ever was assigned to the cell, and then takes not the very brightest ones but one standard deviation up from the mean brightness as the reference brightness, to cut off the very bright anomalous pixels.
And here we come to the actual comparison that tries to tell, which results are better and which are worse. The trouble is that in a real recording we don't have the ground truth. Instead the CNMF recognition is used as the assumed ground truth, so the comparison is not really how good the recognition is but how close it is to CNMF. If you make something better than CNMF, you'd get a worse rating than if you match CNMF exactly. This could be resolved by generating the artificial images of known pure signal with noise added on top. And there is a package, NAOMi, that does that. However, unbelievably, NAOMi doesn't save the original profiles it used for generation, producing the CNMF-based recognition as a reference instead, re-creating the same issue.
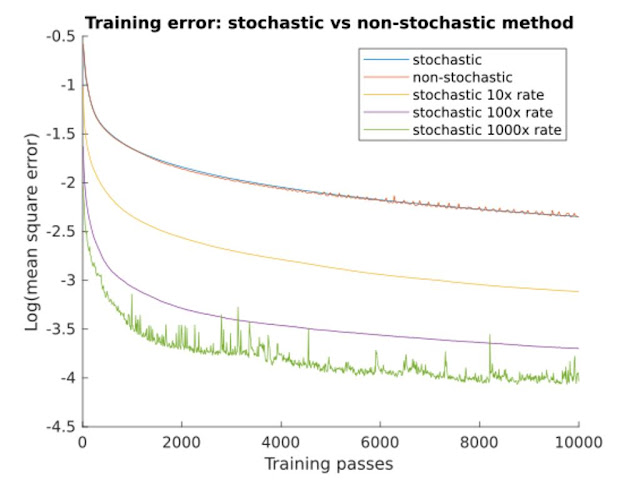
So a consequence of this is that even though SEUDO is supposed to clean up the noise, in reality it produces the best correlation to CNMF when tuned for a very, very mild noise suppression, much milder than the original SEUDO paper found was the optimal trade-off between suppressing the noise and introducing distortion.
Then the comparison by correlation has a couple of fine points. One is that the selection of zero level matters. Raising the zero level cuts off all the lower fluctuations, and doesn't scale with the correlation's normalization. The best correlation will be with the same selection of zero level.
Another is that the lateral shifts on time axis matter a lot. The very first step of noise suppression in realSEUDO is done by averaging a few frames, and the way it tags the averaged frames is off-center, by the last included frame. So shifting the trace to almost center the averaging makes a big improvement on the correlation. Not quite centering though, for the best result it still has to lag by a frame. Which makes me think that this lag by one frame (or another way to put it, off-by-one difference in frame numbering) is also built into CNMF that is used as the reference.
But comparing the time profiles is insufficient in evaluating the match, the shape of the cells matters too. Figure 4 in the appendix to realSEUDO paper contains a small example of matching profiles together with cell shapes as detected by different algorithms. This is a small subset of the full matching that was auto-generated. It's technically a post-processing, not a part of realSEUDO, but if we want to compare the different algorithms, we need to build some automated ways to find the differences in their outputs. Our version of differencing reused a part of the realSEUDO logic. Unlike correlation that produces a close-or-not score, realSEUDO's evaluation differentiates separate cases, with a score for what it thinks is the best fitting case:
- Two shapes are unrelated
- One image subsumes another closely enough to be two versions of the same image
- One image subsumes another and is a combination of multiple images
- Two shapes overlap but are distinct
Just as realSEUDO uses these scores for merge-or-split decisions, the same can be applied to matching, on both space and time. And so, for example, it recognized that CNMF's cell 35 got found in a similar shape by realSEUDO as cell 4, but by OnACID as two separate cells 7 and 22. Of course, without knowing the ground truth we still can't tell, which way is more correct, other than by eyeballing the video at the times of discrepancies.